Exploring the Binomial Theorem
We want to calculate - to expand - higher powers of binomials, like
![]() = ? How can we do this with DERIVE?
= ? How can we do this with DERIVE?
Edit the expression, then press E for Expand and the ENTER-key, because we don´t need any special expansion.
ThE result is impressive! What is the calculation time? . . . . . . . .
If you press the Ctrl-key together with the ® - key you are able to shift the expression so that you can see the full result. the ¬ - key (+ Ctrl) will bring you back again.
Write down here the 1st term of the expression: .......................
the 4th one: .................... and the last one: ....................
Let now DERIVE expand the powers of (a + b) and note only the coefficients of the terms. (Write down the numbers neatly one beneath the other):
n = 4: ![]() :
:
n = 5: ![]() :
:
n = 6: ![]() :
:
n = 7: ![]() :
:
If you believe to recognize a system, then add two lines more (for n = 8 and 9). Check the numbers with DERIVE. If you don´t see a system, then don´t worry, let DERIVE do the work.
Complete the scheme of numbers upwards (n = 3, 2, 1)
How should the prime line (n = 0) look like? ...........................
Which conclusion can be drawn from this line? Check it!
.............................................................................................................................................
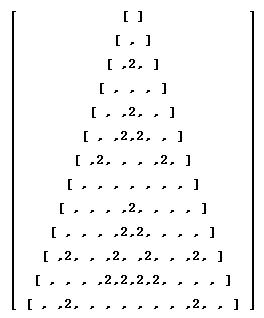
| Write down the numbers from the coefficients´ scheme in form of a triangle: | |
| (n = 0) |
1
1 1 1 2 1 |
| (n = 1) | |
| (n = 2) | |
| (n = 3) | |
| (n = 4) | |
| (n = 5) | |
| (n = 6) | |
| (n = 7) | |
| (n = 8) | |
| (n = 9) | |
| (n = 10) | |
| (n = 10) | |
| (n = 11) | |


(Both pictures from the - highly recommended - book AGNESI to ZERO, Key Curriculum Press)
Form the sum of the numbers in each line!
What can you notice? ..............................................................................................................
Are you able to proof this facts? (A hint: substitute for a and b!)
...............................................................................................................................................
Observe the exponents of a and b in the partial expressions of the expansions of the first five powers of (a + b).
Try to generate (a + b)8 using PASCAL´s Triangle. >Then check your result with DERIVE.
(a + b)8 = .............................................................................................................................
Try your experience at (2x + 3y)5:
(2x + 3y)5 = .........................................................................................................................
Expand all the partial
expressions:
...............................................................................................................................................
Check again with DERIVE:
Expand (a + b)5 , then we replace (substitute) in the result for a and b the values 2x and 3y in the following way:
Highlight the result of (a + b)5, then perform a substitution. DERIVE will ask you now to substitute for all variables which can be found in the highlighted expression. If you don´t want to substitute for any variable then press ENTER, in the other case you substitute the offered variable by your special quantity.
Here for a: 2x and for b: 3y. Compare the result offered by DERIVE with yours one! Expanding this will lead to a final result. You can let expand (2x + 3y)5 directly without intermediate substitution.
Try now (4z + 2u)6 = ................................................................................................ =
= ...........................................................................................................................................
and compare with the CAS-result!
Which is the effect of the changed sign in (a - b)n? Express your findings in your own words:............................................................................................................................
| (z + 4)6 | = ................................................................................................. = |
| = ..................................................................................................... | |
| (4x2y -3xy3)8 | = ....................................................................................................................... |
| = ....................................................................................................................... | |
| (5ab + 2 b2)9 | the 3rd element: ...................; the 7th element: ....................... |
| (2u + 1,5a)5 | = ...................................................................................................................... |
| Find a way to expand (3 a2 - 2 a b + b2)5? | |
| ............................................................................................................................................... | |


Start a new DERIVE session and then load the utility file PASCAL.MTH in the background.

| pas_di(n,a) | generates the first n rows of P.T; all elements, which are divisible by a will be represented by a *, the others by a space. (eg: pas_di(25,2)). Which n will "fit into your screen"? |
| pas_div(n,a) | represents the numbers from above by 0 and 1. |
| pas_rem(n,a,r) | marks all numbers of the P.T., which leave the remainder r after a division by a. |
| pas_rm(n,a,r) | mark these positions with a *, eg. pas_rn(15,5,2) |
| pas_rems(n,a) | shows all remainders after a division by a, eg pas_rems(15,5). |

These nice fractals can easily be produced on the TI-89/92 screens using a short programm (see below)
Using the two programs pas() und invpas() you can generate various "pictures" emerging from Pascal´s Triangle..
Transmit both programs pas and invpas und das Hilfsprogramm pt auf dein Gerät.
pas(n,divisor,remainder)
paints all locations in the first n rows of the P.T. where the division
of the number by divisor leaves the remainder.
invpas(n,divisor,remainder)
returns black at these positions, where we do not receive the remainder.
If one wants to mark
the even coefficients in the first 10 rows then call pas(10,2,0).
Why?
Try to reproduce your hand made paintings on the TI screen. How many rows can be represented on this small screen?
Which parameters in pas generate the following pictures?

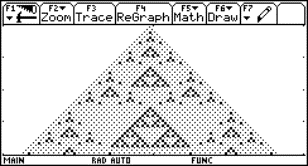
Try to produce two "extra nice" Pascal pictures.
My Pascal Gallery:
The program code for pas(n,a,r):
pas(n,a,r)
Prgm
ClrDraw
FnOff :PlotsOff
setGraph("Axes","Off")
setGraph("Grid","Off")
Local i,j,z,pt
Define pt(x,y)=Prgm
PxlOn x,y:PxlOn
x,y:PxlOn x+1,y
PxlOn x,y-1:PxlOn
x+1,y-1
EndPrgm
For i,0,n
For j,0,i
nCr(i,j)»z
If mod(z,a)=r
Then
pt(1+2*i,117-2*i+4*j)
Else
PxlOn 1+2*i,116-2*i+4*j
EndIf
EndFor
EndFor
EndPrgm
Two explanations and one question:
nCr(i,j) generates the "binomial coefficients" using a rule which you will learn later in the frame of probability theory.
Funktion mod(z,a) - Modulo Function - returns the integer remainder after division of the interger z by the integer a.
Find first mentally, then using the TI:
mod(87,9) = ........., mod(15,3) = ........., mod(113,7) = ........., mod(200,13) = .........
Which line of the program above you will have to change to change pas() to invpas()?

Program invpas(n,a,r)
invpas(n,a,r)
Prgm
ClrDraw
FnOff :PlotsOff
setGraph("Axes","Off")
setGraph("Grid","Off")
Local i,j,z,pt
Define pt(x,y)=Prgm
PxlOn x,y:PxlOn
x,y:PxlOn x+1,y
PxlOn x,y-1:PxlOn
x+1,y-1
EndPrgm
For i,0,n
For j,0,i
nCr(i,j)»z
If mod(z,a)r
Then
pt(1+2*i,116-2*i+4*j)
Else
PxlOn
1+2*i,117-2*i+4*j
EndIf
EndFor
EndFor
EndPrgm